Active Brownian motion
When Robert Brown first encountered the scattering motion of small particles on a water surface he first ascribed them to an active force embedded in the particles. At latest the theoretical work by Einstein and Smolunchowski cleared up doubts, that the motion was not caused by random kicks from the surrounding water molecules.
In contrast to those particles moving around passively, active particles have some internal mechanism that influences the motion. For example synthetic Janus swimmers, where the particles are coated in a way that created a propulsion in a certain direction. Due to the propulsion force emulsions of the swimmers are inherently out of equilibrium and thus display a possitive entropy production rate. This result can, however, only be obtained in a model that incorporates the chemical reaction providing the propulsion.
Another example of active particles are bacteria that can reshape in order to implement different modes of motility. For instance E. Coli which can stir attached flagella to either implement a propulsion or a low motility state where orientational changes are more likely resulting in a Run-and-Tumble trajectory. We derive the distribution of its extreme fluctuations and identify its universal properties using large deviation theory.
- Entropy production of active particles and for particles in active baths, P. Pietzonka, and U. Seifert, J. Phys A: Math. Theor. 51, 01LT01 (2018), Abstract, Download
- Extreme fluctuations of active Brownian motion, P. Pietzonka, K. Kleinbeck, and U. Seifert, New J. Phys., 18, 052001 (2016), Abstract, Download
Stochastic (thermo-)dynamics of molecular motors
Molecular motors are enzymes that convert chemical energy into mechanical work e.g. via ATP-hydrolysis. Operating in an aqueous solution, the influence of thermal fluctuations gives rise to stochastic dynamics and energetics. Furthermore, a particle is typically attached to a carried load or an experimental probe particle that makes the motion of the motor visible. Thus, when analyzing experimental data we should take into account that the motor is not observed directly, e.g. by explicitly modeling the elastic coupling between the probe and the motor. The combined dynamics consists of discrete steps of the motor and continuous Brownian motion of the probe. Based on this model, one can analyze the motor efficiency and verify whether a coarse graining to a one-dimensional model retains essential dynamical features. We also demonstrate numerically that the coarse-grained, observable data suffices to recover important parameters like the motor's step width or stalling force.
- Effective rates from thermodynamically consistent coarse-graining of models for molecular motors with probe particles, E. Zimmermann and U. Seifert, Phys. Rev. E 91, 022709 (2015), Abstract, Download
- Fine-structured large deviations and the fluctuation theorem: Molecular motors and beyond, P. Pietzonka, E. Zimmermann, and U. Seifert, EPL 107, 20002 (2014), Abstract, Download
- Efficiencies of a molecular motor: A generic hybrid model applied to the F1-ATPase, E. Zimmermann and U. Seifert, New J. Phys. 14, 103023 (2012), Abstract, Download
- Efficiency of molecular motors at maximum power, T. Schmiedl and U. Seifert, EPL 83, 30005 (2008), Abstract, Download
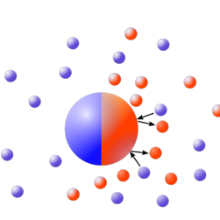
Efficiency of self-propelled particles
Janus particle are pushed forward by a chemical reactions on the surface. Any spacila assymetry in the reaction rate produces a gradient of reactant concentration which in turn leads to a propulsion force. Often such an assymetry is realized by giving one half of a sphere a catalytic coating. We investigate how the gradient of reactant concentration influences the efficieny of the microscopic machines through detailed analytical modeling and optimize their performance.
Related publications
- Nonlinear, electrocatalytic swimming in the presence of salt, B. Sabass and U. Seifert, J. Chem. Phys. 136, 214507 (2012), Abstract, Download
- Dynamics and efficiency of a self-propelled, diffusiophoretic swimmer, B. Sabass and U. Seifert, J. Chem. Phys. 136, 064508 (2012), Abstract, Download
- Efficiency of surface-driven motion: nano-swimmers beat micro-swimmers, B. Sabass and U. Seifert, Phys. Rev. Lett. 105, 218103 (2010), Abstract, Download