Unlike classical thermodynamics, modern stochastic thermodynamics applies to inherently dynamical phenomena such as relaxation, driving and transport processes. Mathematically, these physical features are encoded in the equations of motion within particular models. Thus, studying these specific problems provides not only technical insight, but also the potential for future application.
The Mpemba effect
The observation that, under certain conditions, warm water can take less time to freeze than colder one is one of the most prominent examples of a counterintuitive relaxation phenomenon and known as the Mpemba effect. Turning this experimental insight into a problem of stochastic thermodynamics requires the design of an appropriate mathematical model.
Recently, we introduced an isothermal analog of this effect: By applying a driving force, a system is prepared in a non-equilibrium steady state. When the force is switched off, the system relaxes into thermal equilibrium with its environment. We have shown for a Langevin model that the parameters in which a stronger driving force leads to faster relaxation is indeed - possibly contrary to expectation - quite generic.
Optimal driving in finite time
Transferring a physical system from an inital state to some desired final state while minimizing dissipation is a fundamental issue in thermodynamics. In recent years, stochastic thermodynamics allowed us to revisit classical results like the Landauer bound or Carnot efficiency. We try to gain insight into the fundamental rules of optimal, i.e., dissipation-minimizing, protocols by studying differences between conservative and non-conservative driving on Markov networks. Further, we consider the effects of constraining the degrees of freedom that can be driven by a protocol.
Delayed response in periodically driven systems
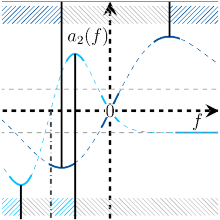
Stochastic thermodynamics studies systems that are exposed to the influence of an environment. If this influence changes in time, the system is considered to be time-dependently driven. These systems form a vast and manifold class ranging from microscopic heat engines to erasure protocols. One property that unites all these quite different systems is some form of lag between the driving of the system and its response. Ultimately, this lag is traced back to the inability of a system to react infinitely fast to external changes.
In order to gain a better understanding for this set of phenomena we need to first model, then quantify it. Having achieved this, the next step is to explore the conceptual and mathematical relations to other quantities of interest. For periodically driven systems, we have succeeded in identifying the lag of our system as a phase-like quantity, i.e., an angular delay variable. We find a relationship between this phase and the relative speed of external driving.
Related publications:
- Phase shift in periodically driven non-equilibrium systems: Its identification and a bound, J. Degünther, T. Koyuk, and U. Seifert, J. Stat. Mech., 033207, 2022, Abstract, Download